$E(uu^{'})=\sigma ^{2}\Omega $
$E(uu^{'})=\sigma ^{2}I$
There are many forms of FGLS, and the following passage describes its basic theorem and one form of FGLS that could eliminate if there is only heteroscedasticity:
Theorem of GLS, WLS, and One Form of FGLS
There is also another model to eliminate only AR(1) pattern in the OLS residuals:
1) Estimate coefficient $\rho$ in the residuals that
$e_{t} = \rho e_{t-1} + \varepsilon$
2) Transfer
$y = X\beta +u $
to
$Py = PX\beta +Pu $
by
and 3) Estimate corresponding
 with OLS estimation.
with OLS estimation.I will add more forms of FGLS in the following if possible.
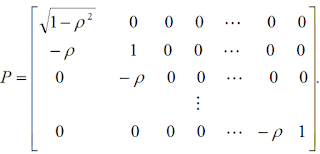
No comments:
Post a Comment